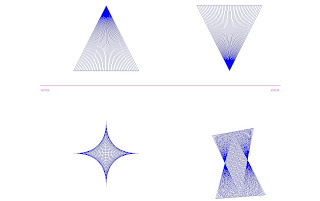
Superficies regladas alabeadas: 2010

Superficies alabeadas son las que se generan por el movimiento de una línea recta, de forma que dos posiciones adyacentes de la recta se cruzan.

Clasificación de las superficies alabeadas: las generatrices deben apoyarse siempre sobre tres directrices:

1- Se apoyan sobre tres directrices sin perder en ningún momento el contacto con ellas.

En este caso tenemos el hiperboloide elíptico y de revolución, construidos sobre tres líneas rectas.

Curvas alabeadas construidas con dos líneas rectas y una curva.

Curvas alabeadas construidas con una línea recta y dos curvas, por ejemplo el cuerno de vaca.

Curvas alabeadas construidas con tres líneas curvas.

2- Se apoyan en dos líneas directrices y siempre están paralelas a un plano director.

Apoyado sobre dos líneas rectas tenemos el paraboloide hiperbólico.

Apoyado en una línea recta y una curva tenemos el conoide y el helicoide recto.

Apoyado en dos líneas curvas tenemos el cilindroide.

3- Se apoyan en dos líneas directrices y forma la generatriz siempre un mismo ángulo con algún plano.

Apoyado en dos líneas rectas tenemos el hiperboloide concoideo

Apoyado en una línea recta y una curva tenemos el helicoide oblicuo.

Apoyado en dos líneas curvas tenemos el helicoide oblicuo.

Todas las superficies alabeadas son siempre regladas, esto quiere decir que se pueden generar con una línea recta. Si en un punto de una superficie reglada sólo se puede trazar una línea recta tangente y no más se dice que la superficie reglada es simple, también denominada regladas simple o de simple reglaje. Si se pueden trazar dos será de doble reglaje. Las superficies de doble reglaje son el hiperboloide elíptico y el paraboloide hiperbólico.

El paraboloide hiperbólico

El paraboloide hiperbólico está generado por una recta que se apoya en dos líneas directrices y siempre se mantiene paralela a un plano llamado director. Existe otro conjunto de generatrices consideradas como directrices y un plano paralelo a estas directrices definido como nuevo plano director.
Dos generatrices infinitamente próximas se cruzan mientras que las de distinto sistema se cortan.
La superficie es de segundo orden ya que si es cortada por una recta la corta como máximo en dos puntos.
El plano tangente en un punto a la misma está definido por dos generatrices, una de cada sistema, y ambas pasan por el plano.
Como cada sistema contiene una generatriz en el infinito -la línea del infinito del plano director- todo plano secante tiene dos puntos en el infinito comunes con la superficie. Las secciones planas de la superficie son de forma general hipérbolas y en casos particulares parábolas.
Los planos paralelos a la recta común de los planos directores producen secciones parabólicas mientras que todas las demás secciones son hiperbólicas.

2 paraboloides hiperbólicos en cada cubo (uno en azul y otro en rojo), de distinta torsión pero con las mismas directrices (2 rectas).

El conoide

El conoide es una superficie reglada alabeada con un plano director y dos directrices, una rectilínea y otra curva. Si la directriz curva es un círculo se tiene el conoide circular, si es una elipse tenemos el conoide elíptico, etcétera.
Si la recta directriz es paralela al plano de la directriz curva y perpendicular al plano director la superficie engendrada se denomina conoide recto, en caso de que no lo sea se denomina oblicuo.

2 semiconoides (uno en azul y otro en negro), de distinta torsión pero con las mismas directrices (una semielipse y una recta).

Hiperboloide de revolución de una rama.

Se le denomina también hiperboloide y es un caso particular del hiperboloide elíptico.

Todas las secciones que cortan a la superficie perpendicularmente al eje son círculos. El hiperboloide se puede generar por una recta que se mueve siempre en contacto con tres directrices que se cruzan, también por una recta girando alrededor del eje de forma que se cruza con él. También se puede generar por una recta que se mueve incidente en tres círculos cuyos centros están en el eje de revolución. También se puede generar por una hipérbola que gira alrededor de la directriz.

Siendo el hiperboloide de doble reglaje se puede construir mediante el cruzado de barras rectas. Se aplica en torres, mástiles, en tejidos, engranajes hiperbólicos para dos ejes que se cruzan. Las superficies de rodadura son troncos de hiperboloides. Los dientes de engranajes hiperbólicos en forma de espiral para suavizar la acción motriz del sistema de engranajes.

Si consideramos dos rectas que se cruzan y una de ellas es el eje de revolución al girar las se engendra un hiperboloide de una hoja.
Las rectas de esta superficie infinitamente próximas se cruzan y la simétrica de cualquiera respecto a un plano meridiano de la superficie de revolución es una generatriz del otro sistema de rectas.
El hiperboloide es una superficie cuyas secciones son siempre cónicas, cuando la superficie gira cualquier generatriz aparece dos veces paralela a un plano meridiano por lo que toda sección meridiana es una hipérbola. De ello se desprende que la superficie se puede generar por rotación de una hipérbola en torno a su eje.
El hiperboloide es una superficie de segundo orden y por cada uno de sus puntos pasan dos líneas de cada sistema que definen el plano tangente en uno de sus puntos. Éste plano secciona a la superficie en dos rectas. La superficie no se puede desarrollar por ser alabeada.

Para calcular la intersección de una superficie alabeada como un plano se unen los puntos de intersección de las generatrices con el plano secante.
La intersección de cualquier superficie alabeada con otra se obtiene calculando las intersecciones de las generatrices de las dos.

Las superficies regladas alabeadas encuentran una aplicación muy extendida en la construcción de cubiertas, tejados, ajustes de tuberías, engranajes, torres de refrigeración de centrales nucleares, engranajes hiperbólicos para ajustar ruedas cuyos ejes se cruzan, etc.

El helicoide

El helicoide recto es una superficie reglada alabeada cuya generatriz se mueve siempre en contacto con dos hélices concéntricas. Estas hélices son sus directrices y forman un ángulo siempre igual con sus ejes. Si la generatriz es ortogonal tenemos un helicoide recto, si no lo es porque tenemos uno público. El helicoide recto que tiene una generatriz incidente en el eje entra dentro de la clasificación del conoide, ya que todos sus elementos son paralelos al plano director.

El helicoide oblicuo es aquel cuya generatriz siempre mediante un mismo ángulo.

La superficie helicoidal posee muchas aplicaciones, la rosca cuadrada con una helicoidal posee una superficie lateral que es un helicoide recto, los muelles de arrollamientos helicoidales. Las roscas de tornillos los muelles de las bobinas, los resortes, las rocas de los taladros las escaleras de caracol, etcétera.

Cuerno de vaca